Gekoppelte Fahrzeuge¶
Aufgabenstellung¶
Zwei aneinander gekoppelte Fahrzeuge mit den Masse \(m_1\) und \(m_2\) befinden sich in Ruhe. Zwischen beiden Fahrzeugen befindet sich eine nicht befestigte und um die Länge \(x\) zusammengedrückte Feder der Federkonstanten \(k\). Nach Lösen der Kopplung entspannt sich die Feder.
Aufgabe 1: Welche Geschwindigkeiten \(v'_1\) und \(v'_2\) besitzen danach die beiden Fahrzeuge? (für beliebige Massen) Man betrachte Energie und Impuls in einem System, das sich mit dem Schwerpunkt bewegt.
Aufgabe 2: Es sei \(m_1 = m_2 = m\). Welche Konsequenz ergibt sich dadurch für die Geschwindigkeiten \(v'_1\) und \(v'_2\) und wie groß sind sie?
Gegeben¶
Masse der Fahrzeuge \(m_1 = m_2 = m = 500~kg\)
Längenänderung der Feder beim Zusammendrücken \(x = 0,16~m\)
Federkonstante \(k = 40~\frac{kN}{m}\)
Gesucht¶
Geschwindigkeit in Metern pro Sekunde \(v'_1\), \(v'_2\) [\(\frac{m}{s}\)]
Skizze¶
Physikalischer Lösungsweg¶
benötigt: Energieerhaltungssatz EES und Impulserhaltungssatz IES
Formeln
\(v_1' = -\frac{m_2}{m_1} \cdot v_2'\)
\(v_2' = \Delta x \sqrt{\frac{k \cdot m_1}{m_2^2 + m_1 \cdot m_2}}\)
daraus folgt:
\(v_1' = - \frac{m_2}{m_1} \cdot \Delta x \sqrt{\frac{k \cdot m_1}{m_2^2 + m_1 \cdot m_2}}\)
Berechnung \(v_1'\):
\(v_1' = - 0,16~\rm m \cdot \sqrt{\frac{40000~\rm N/m \cdot 500 ~\rm kg }{(500 ~\rm kg )^2 + 500 ~\rm kg \cdot 500 ~\rm kg }} = - 0,16~\rm m \cdot \sqrt{\frac{20000000 ~\rm Nkg/m}{500000 ~\rm kg^2}} = - 0,16~\rm m \cdot 2\sqrt{10~ \rm s^{-2}} = -1,01~\frac{m}{s}\)
daraus folgt \(v_2' = 1,01~\frac{m}{s}\). Dieses Fahrzeug fährt also in die entgegengesetzte Richtung zum ersten Fahrzeug.
Implementierung in Python¶
Zuerst müssen einige Bibliotheken importiert werden, die für Berechnungen, Visualisierung, etc. notwendig sind.
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
Nun werden die gegebenen Werte als Variablen definiert.
# Definieren der Variablen
m1 = 500 # Fahrzeuggewicht [kg]
m2 = 500 # Fahrzeuggewicht [kg]
x = 0.16 # zusammengedrückte Feder [m]
k = 40000 # Federkonstante [N/m] -> 40 kN/m
# Funktion zur Berechnung von v1'
def berechne_v1(m1, m2, x, k):
v1 = -(m1/m2) * x * ((k * m1)/(m2**2 + (m1*m2)))**0.5
return v1
def berechne_v2(m1, m2, x, k):
v2 = x * ((k * m1)/(m2**2 + (m1*m2)))**0.5
return v2
# Verwendung der Funktion
v1 = berechne_v1(m1, m2, x, k)
v2 = berechne_v2(m1, m2, x, k)
print(f"v1' beträgt {round(v1, 2)} m/s und v2' beträgt {round(v2, 2)} m/s")
v1' beträgt -1.01 m/s und v2' beträgt 1.01 m/s
Graphische Darstellung unter Variation der Anfangsbedingung¶
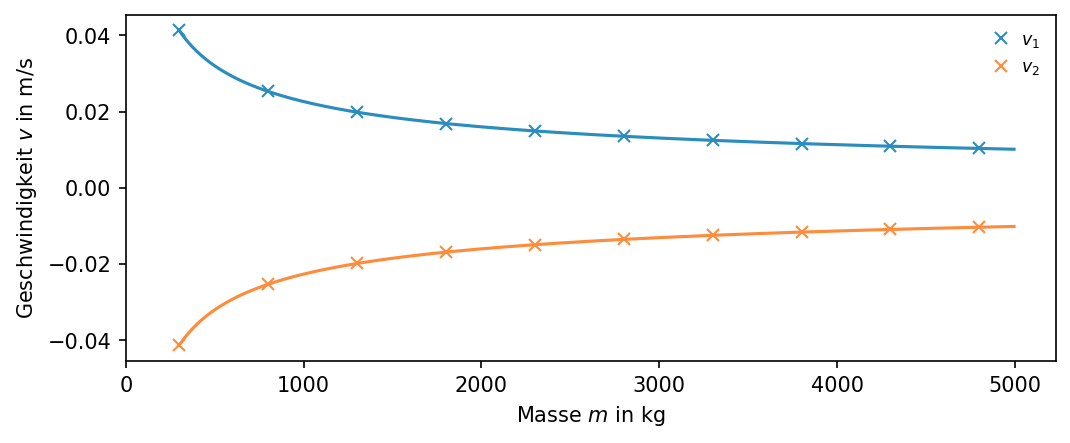
Nun können beispielsweise die Geschwindigkeiten für verschiedene Fahrzeug-Massen errechnet werden. In einem ersten Schritt wird hierbei wieder ein Vektor mit unterschiedlichen Massewerten erstellt und anschließend \(v_1\)’ und \(v_2\)’ für jeden Wert berechnet.
# Erstellen eines Vektors
m_vector = np.arange(300, 5000, 500)
# Initialisierung einer Liste für die berechneten Werte
values = []
for m_i in m_vector:
k = 40 # Federkonstante [kN/m]
v1 = berechne_v1(m_i, m_i, x, k)
v2 = berechne_v2(m_i, m_i, x, k)
values.append([m_i, v1, v2])
values_table = pd.DataFrame(values, columns=['Masse in kg', 'v1 in m/s', 'v2 in m/s'])
values_table.head() #.head -> nur die ersten Zeilen werden angezeigt
| Masse in kg | v1 in m/s | v2 in m/s | |
|---|---|---|---|
| 0 | 300 | -0.041312 | 0.041312 |
| 1 | 800 | -0.025298 | 0.025298 |
| 2 | 1300 | -0.019846 | 0.019846 |
| 3 | 1800 | -0.016865 | 0.016865 |
| 4 | 2300 | -0.014920 | 0.014920 |
# Definieren der Größe und des Aussehens des Plots
plt.figure(num=None, figsize=(8, 3), dpi=150, facecolor='w', edgecolor='k')
plt.plot(values_table['Masse in kg'], values_table['v2 in m/s'], 'x', color='#2b8cbe')
plt.plot(values_table['Masse in kg'], values_table['v1 in m/s'], 'x', color='#fd8d3c')
plt.plot(np.arange(300, 5000, 5), berechne_v2(np.arange(300, 5000, 5),np.arange(300, 5000, 5),x,k), '-', color='#2b8cbe')
plt.plot(np.arange(300, 5000, 5), berechne_v1(np.arange(300, 5000, 5),np.arange(300, 5000, 5),x,k), '-', color='#fd8d3c')
plt.xlabel(r"Masse $\mathit{m}$ in kg")
plt.xlim(xmin = 0)
plt.ylabel(r"Geschwindigkeit $\mathit{v}$ in m/s")
plt.legend(['$v_1$', '$v_2$'], frameon=False, handlelength=0.75, fontsize='small')
plt.show()
Nun können wir natürlich auch davon ausgehen, dass die zwei Fahrzeuge unterschiedliche Massen besitzen:
# Vektoren für unterschiedliche Massen der Fahrzeuge
m1_vector = np.arange(300, 900, 100)
m2_vector = np.arange(50, 350, 50)
# Initialisierung einer Liste für die berechneten Werte
values = []
# Berechnung von Kraft und Querkontraktion
for m1_i, m2_i in zip(m1_vector, m2_vector):
v1 = berechne_v1(m1_i, m2_i, x, k)
v2 = berechne_v2(m1_i, m2_i, x, k)
m_ges = m1_i + m2_i
values.append([m1_i, m2_i, m_ges, v1, v2])
values_table = pd.DataFrame(values, columns=['m1 in kg', 'm2 in kg', 'm gesamt in kg', 'v1 in m/s', 'v2 in m/s'])
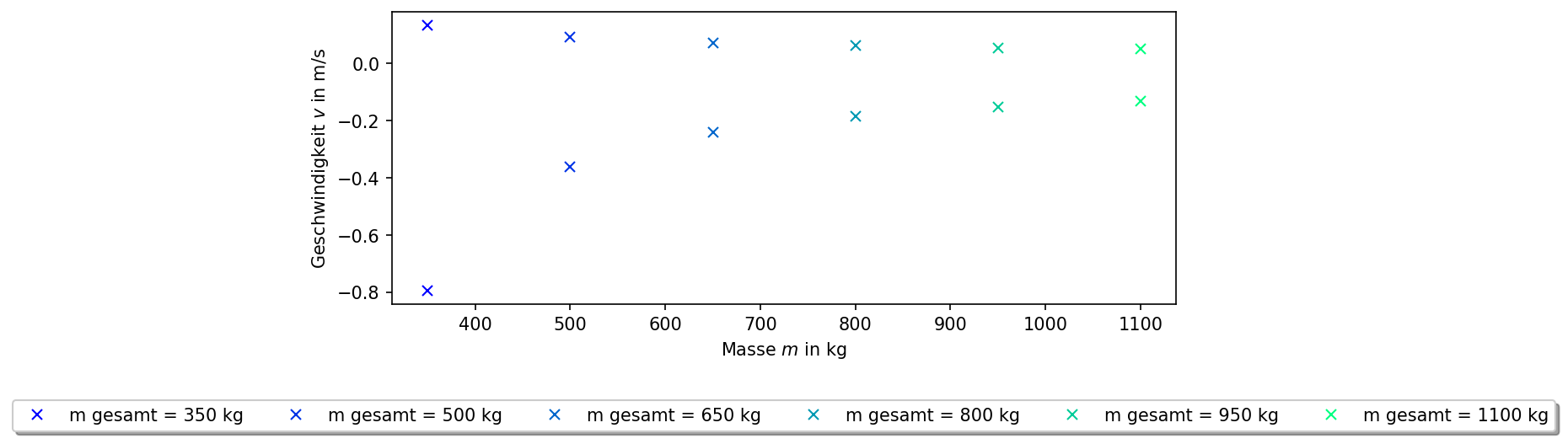
values_table
| m1 in kg | m2 in kg | m gesamt in kg | v1 in m/s | v2 in m/s | |
|---|---|---|---|---|---|
| 0 | 300 | 50 | 350 | -0.794956 | 0.132493 |
| 1 | 400 | 100 | 500 | -0.362039 | 0.090510 |
| 2 | 500 | 150 | 650 | -0.241552 | 0.072466 |
| 3 | 600 | 200 | 800 | -0.185903 | 0.061968 |
| 4 | 700 | 250 | 950 | -0.153824 | 0.054937 |
| 5 | 800 | 300 | 1100 | -0.132864 | 0.049824 |
# Für die Visualisierung werden nun die verschiedenen Messungen anhand von m1 gruppiert
groups = values_table.groupby("m gesamt in kg")
# Definition einer Farbpalette
col_pal = plt.get_cmap('winter', len(m1_vector))
# Initialisieren einer Zählvariable
i = -1
# Definieren der Größe und des Aussehens des Plots
plt.figure(num=None, figsize=(8, 3), dpi=150, facecolor='w', edgecolor='k')
# Iteration der a0 Gruppen und anschließende Visualsierung der Zeitverläufe
for name, group in groups:
i = i+1
plt.plot(group['m gesamt in kg'], group['v2 in m/s'], 'x', color=col_pal(i), label = f"m gesamt = {name} kg") #, $m2 = ${group['m2', i]
plt.plot(group['m gesamt in kg'], group['v1 in m/s'], 'x', color=col_pal(i)) #label = f"$m1 = ${name} "
#plt.plot(values_table['m gesamt'], values_table['v2'], 'x', color='#2b8cbe')
#plt.plot(values_table['m gesamt'], values_table['v1'], 'x', color='#fd8d3c')
# plt.plot(values_table['m gesamt'], values_table['v2'], '-', color='#2b8cbe')
# plt.plot(values_table['m gesamt'], values_table['v1'], '-', color='#fd8d3c')
plt.xlabel(r"Masse $\mathit{m}$ in kg")
#plt.xlim(xmin = 300)
plt.ylabel(r"Geschwindigkeit $\mathit{v}$ in m/s")
plt.legend(loc='upper center', bbox_to_anchor=(0.5, -0.3),fancybox=True, shadow=True, ncol=len(m1_vector))
#plt.legend(['$v_1$', '$v_2$'], frameon=False, handlelength=0.75, fontsize='small')
plt.show()