Einführung¶
In diesem Einführungsskript wird der Aufbau der PyVo-Aufgaben erklärt, ebenso wie eine simple Aufgabe mittels Programmierung gelöst.
Die Aufgabenstellung wird als erstes notiert. Daraus lassen sich alle gegebenen und gesuchten Werte extrahieren.
Aufgabenstellung¶
Ein Auto legt innerhalb von 3 Minuten eine Strecke von 1,9 km zurück. Wie schnell fährt es?
Gegeben¶
zurückgelegte Strecke \(s = 1,9~km\)
Zeit \(t = 3~min\)
Gesucht¶
Geschwindigkeit \(v\) in \(\frac{m}{s}\)
Skizze¶
An dieser Stelle ist eine Skizze zur Visualisierung der Aufgabenstellung vonnöten. Alle gegebenen und gesuchten Werte werden in diese Skizze eingeführt.
Physikalischer Lösungsweg¶
Hier werden nun die benötigten Formeln zur Berechnung aufgeführt. Die Formel der gleichförmigen Bewegung benötigt die Informationen zur Strecke \(s\), Geschwindigkeit \(v\), Zeit \(t\) und Anfangsweg \(s_0\).
\(s = v \cdot t +s_0\)
mit \(s_0\) für den Anfangsweg in Meter. Wenn der Anfangswegs nicht gegeben ist, so vereinfacht sich die Formel zu:
\(s = v \cdot t\)
Durch Umstellen dieser Gleichung erhält man die Formel für die Geschwindigkeit \(v\):
\(v = \frac{s}{t}\)
Nun können die oben gegebenen Werte in diese Gleichung eingesetzt werden:
\(v = \frac{1900}{180} = 10,6~\frac{m}{s} = 38,2~\frac{km}{h}\)
Implementierung in Python¶
Bei komplexen Aufgaben und bei der Variation von bestimmten Komponeten kommt man mit der händischen Berechnung schnell an seine Grenzen. Um dennoch solche Probleme zu lösen, können Programmiersprachen wie Python verwendet werden. Die PyVo-Skripte, die im Folgenden vorgestellt werden, sollen dabei helfen diverse physikalische Problemstellungen zu berechnen, zu analysieren und zu visualisieren.
Für die Ausführung eines PyVo-Skriptes, ist es nötig direkt zu Beginn nötige Bibliotheken zu importieren. Dazu zählen beispielweise Bibliotheken zur Erstellung von graphischen Darstellungen oder spezielle Bibliotheken zur Erstellung von Tabellen und Vektorrechnung. Sollte man im Laufe des Programmierens eine Bibliothek hinzufügen, ist es von Vorteil, diese direkt an den Anfang des Skripts zu schreiben. So werden diese direkt zu Beginn der Skriptausführung geladen.
# Verwaltung von Daten und deren Analyse
# enthält Datenstrukturen und Operatoren für den Zugriff auf numerische Tabellen und Zeitreihen
import pandas as pd
# für die Visualisierung von Daten
import matplotlib.pyplot as plt
# für eine einfache Handhabung von Vektoren oder Matrizen
# besitzt implementierte Funktionen für numerische Berechnungen
import numpy as np
# wichtige Funktion für mathematischen Operationen
import math
Nun kann die oben definierten Formeln als Funktionen definiert werden. Diese Funktion kann im Laufe des Skripts immer wieder verwendet werden.
# Funktion zur Berechnung der Geschwindigkeit
def berechne_v(s, t):
return s/t
# Funktion zur Berechnung der Strecke
def berechne_s(v,t):
return v*t
Mittels der Funktion “berechne_v()” kann nun die Geschwindigkeit \(v\) berechnet werden. Hierfür müssen allerdings die gegebenen Werte in Variablen gespeichert sein.
# Variablen definieren
s = 1900 # meter
t = 180 # sekunden
# Funktionsaufruf zur Berechnung von v
v = berechne_v(s, t)
# Ausgabe des Ergebnisses unter Beachtung der signifikanten Stellen der Eingabeparameter
print(f"v = {round(v,1)} m/s")
v = 10.6 m/s
Graphische Darstellung¶
Nun können wir die Zusammenhänge für die gegebenen Parameter visualisieren. So ist es einerseits möglich die physikalische Lösung zu visualisieren oder graphische Darstellungen zu erstellen, bei welchen die Anfangsbedingungen verändert werden.
Graphische Darstellung der physikalischen Lösung¶
Im Folgenden soll die zurückgelegte Strecke gegenüber der Zeit aufgetragen werden. Hierfür kann zuerst eine Tabelle erstelt werden, in welcher die Werte stehen, die anschließend visualisiert werden. Diese Tabelle wird aus drei Spalten bestehen: eine Spalte für die Zeitschritt \(t\) in \(s\), eine Spalte für die Geschwindigkeit \(v\) in \(\frac{m}{s}\) und eine Spalte für die zurückgelegte Strecke für jeden Zeitschritt \(s\) in \(m\):
# Erstellen eines Vektors mit Zeitschritten
zeitschritte = np.arange(0, 190, 10)
# Variable der Geschwindigkeit v definieren (diese verändert sich nicht)
v = 10.6
# Erstellen einer leeren Liste
data = []
# Schleife über alle Zeitschritte
for i in zeitschritte:
s = berechne_s(v, i)
data.append([i, v, s])
# Erstellen der Tabelle und Anzeigen der ersten 5 Zeilen
tabelle = pd.DataFrame(data, columns=["Zeitschritt t in s", 'Geschwindigkeit v in m/s', 'Strecke s in m'])
tabelle.head()
| Zeitschritt t in s | Geschwindigkeit v in m/s | Strecke s in m | |
|---|---|---|---|
| 0 | 0 | 10.6 | 0.0 |
| 1 | 10 | 10.6 | 106.0 |
| 2 | 20 | 10.6 | 212.0 |
| 3 | 30 | 10.6 | 318.0 |
| 4 | 40 | 10.6 | 424.0 |
# Definieren der Größe und des Aussehens des Plots
plt.figure(num=None, figsize=(6, 3), dpi=150, facecolor='w', edgecolor='k')
# Auftragen der Strecke gegen die Zeit
plt.plot(tabelle['Zeitschritt t in s'], tabelle['Strecke s in m'], '-')
plt.margins(0,0)
# Achsenbeschriftungen hinzufügen
plt.xlabel(r"Zeit $\mathit{t}$ (s)")
plt.ylabel(r"Strecke $\mathit{s}$ ($m$)")
Text(0, 0.5, 'Strecke $\\mathit{s}$ ($m$)')
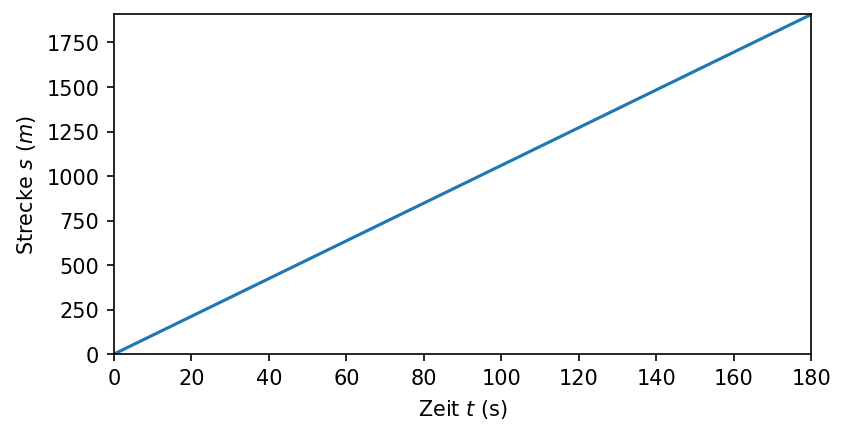
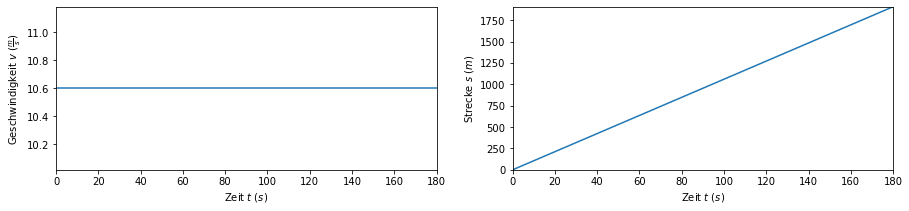
Im Folgenden soll dargelegt werden, dass mehrere Plots zur gleichen Zeit visualisiert werden können. Diese sogenannten Subplots können neben- sowie untereinander dargestellt werden. Hier werden zwei Plots nebeneinander dargestellt. In dem ersten Schritt wird die Geschwindigkeit über die Zeit und im zweiten Plot die Strecke über die Zeit (wie oben schon dargestellt) aufgetragen.
fig, axs = plt.subplots(1, 2, figsize=(15,3))
# Zeichnen der Verläufe
# 1. Plots
axs[0].plot(tabelle['Zeitschritt t in s'], tabelle['Geschwindigkeit v in m/s'])
# 2. Plots
axs[1].plot(tabelle['Zeitschritt t in s'], tabelle['Strecke s in m'])
# Achsenbeschriftung und -begrenzung des 1. Plots
axs[0].set_ylabel(r"Geschwindigkeit $\mathit{v}$ ($\frac{m}{s}$)")
axs[0].set_xlabel(r"Zeit $\mathit{t}$ (${s}$)")
axs[0].set_xlim([min(tabelle['Zeitschritt t in s']),max(tabelle['Zeitschritt t in s'])])
# Achsenbeschriftung und -begrenzung des 2. Plots
axs[1].set_ylabel(r"Strecke $\mathit{s}$ ($m$)")
axs[1].set_xlabel(r"Zeit $\mathit{t}$ (${s}$)")
axs[1].set_xlim([0,max(tabelle['Zeitschritt t in s'])])
axs[1].set_ylim([0,max(tabelle['Strecke s in m'])])
# Anzeige des gesamten Plots
plt.show()
Graphische Darstellung unter Variation der Anfangsbedingung¶
Der Vorteil einer Programmiersprache wie Python ist es, dass wir nun die gegebenen Werte verändern oder auch die Geschwindigkeiten für mehrere Startparameter berechnen können.
So werden im Folgenden die gegebenen Werte für die Zeit verändert.
# Definition verschiedener Zeiten von 180 - 360 bei gleichbleibender Strecke
t_vektor = [180, 200, 220, 240, 260, 280, 300, 320, 340, 360]
# alternative:
# t_vektor = np.arange(180, 380, 20)
# Die zurückgelegte Strecke soll gleich bleiben:
s = 1900
# erneute Definition einer Liste, in der die gemessenen Werte erfasst werden:
messwerte = []
for t_i in t_vektor:
v = berechne_v(s, t_i)
messwerte.append([t_i, v, s])
# Als letztes werden die Messwerte in ein Tabelle konvertiert
tabelle2 = pd.DataFrame(messwerte, columns=['Zeit', 'Geschwindigkeit', 'Strecke'])
tabelle2
| Zeit | Geschwindigkeit | Strecke | |
|---|---|---|---|
| 0 | 180 | 10.555556 | 1900 |
| 1 | 200 | 9.500000 | 1900 |
| 2 | 220 | 8.636364 | 1900 |
| 3 | 240 | 7.916667 | 1900 |
| 4 | 260 | 7.307692 | 1900 |
| 5 | 280 | 6.785714 | 1900 |
| 6 | 300 | 6.333333 | 1900 |
| 7 | 320 | 5.937500 | 1900 |
| 8 | 340 | 5.588235 | 1900 |
| 9 | 360 | 5.277778 | 1900 |
Nun können wir diese Werte in einem einfachen Plot darstellen:
# Definieren der Größe und des Aussehens des Plots
plt.figure(num=None, figsize=(6, 3), dpi=150, facecolor='w', edgecolor='k')
# Auftragen der Scheibendicken gegen die Außentemperatur
plt.plot(tabelle2['Zeit'], tabelle2['Geschwindigkeit'], '-')
plt.margins(0,0)
# Achsenbeschriftungen hinzufügen
plt.xlabel(r"Zeit $\mathit{t}$ (s)")
plt.ylabel(r"Geschwindigkeit $\mathit{v}$ ($\frac{m}{s}$)")
plt.show()
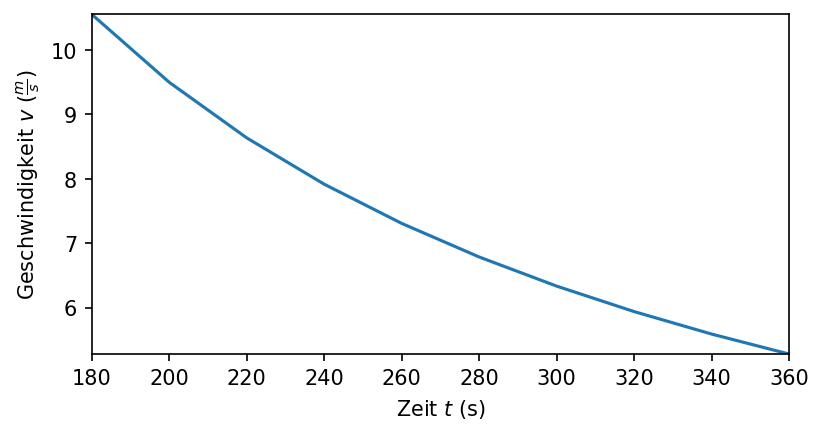
Alle folgenden PyVo Aufgaben werden denselben Aufbau wie hier vorgestellt besitzen.
